- Messages
- 6,180
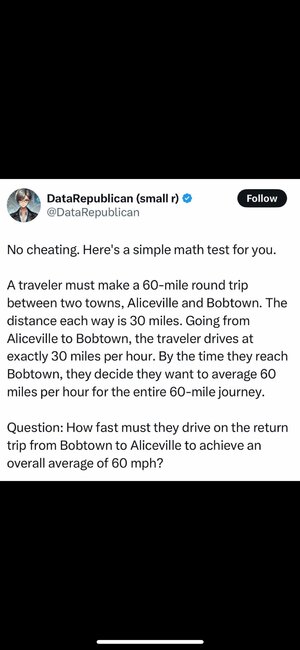
Lot of people are saying this is a trick question as it's impossible, but it's not. I'll admit this got me scratching my head for 30 mins. or so though before I was finally able to put all the pieces together.
So, let's get the obvious out of the way. Total distance is 60 miles. Person drove the first half of the journey at 30 mph. They now want an average of 60 mph. What's the speed they need to drive to achieve that? Well, as we all know, you find the average by taking all the numbers and dividing them by the amount of numbers there are. In this case, we have two numbers. 30 mph and x mph. (30+x)/2=60 is our equation. We multiply 60 by 2 then, get 120, then subtract 30 from 120. We get 90 mph then for x.
But stop right there, criminal scum! We (seemingly) violated the laws of physics. In order to go 60 mph, we need to travel 60 miles in one hour of course, and we already spent an hour going 30 mph which is not the full 60 miles we need. But remember, the question says the person wants to go an average of 60 mph. Not go 60 mph exactly, the whole trip. That would add a time constraint which the question does not actually stipulate.
But wait! Speed is distance over time. So if we add our total distance and time taken to do 30 mph for 30 miles, and 90 mph for the last 30 miles, we should get a 60 mph figure, but we instead get a total of 60 miles over 80 minutes! Clearly then this is impossible and we now need to factor in teleportation and light speed...
Ok, Stephen Hawking. That won't be necessary. In order to achieve the desired average speed, we either need to go 60 miles for 1 hour, or 120 miles for 2 hours. "But that still doesn't make sense," you might say. "Even with that, the total distance covered in the total time taken still does not equal 120 miles over 2 hours. Yes, that is true, but that's because you cut the trip short before it could go to the 120-mile mark. Let's imagine the trip as a 120-mile line from A to B. You go a certain speed at point A and finish at a different speed at point B. You can then put a point anywhere on that line and calculate what the exact distance traveled over time was. If we go 30 mph for 30 miles, and then 90 mph, for the rest of the 90 miles, at the exact time we hit point B, we will have an exact average speed of 60 mph.
BUT... If we cut the line to be half that, and we're still going 30 mph for 30 miles, then by the time we hit the 60-mile mark, we would not have traveled a sufficient distance to bring our exact average speed at that time to 60 mph. Nevertheless, as we go further and further beyond the 60-mile mark, our distance increase will outpace our time increase until we finally hit an average of 60 mph.
BUT... If we cut the line to be half that, and we're still going 30 mph for 30 miles, then by the time we hit the 60-mile mark, we would not have traveled a sufficient distance to bring our exact average speed at that time to 60 mph. Nevertheless, as we go further and further beyond the 60-mile mark, our distance increase will outpace our time increase until we finally hit an average of 60 mph.
Last edited:

